Obliczanie objętości i pól powierzchni brył nieobrotowych ograniczonych powierzchniami prostokreślnymi

Niejednokrotnie w praktyce projektanta - architekta, inżyniera - pojawia się potrzeba obliczenia kubatury, czyli objętości bryły budynku, który nie jest bryłą obrotową.

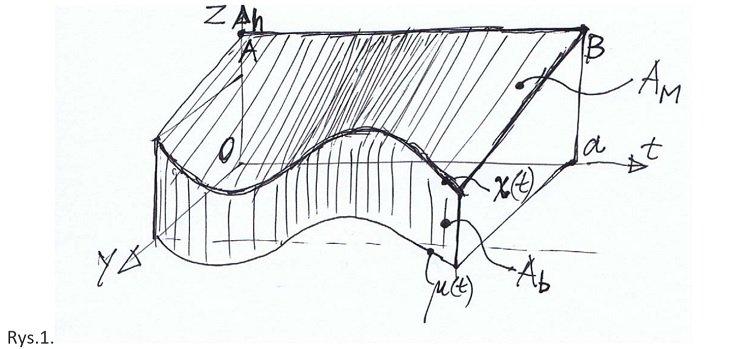
Bywa taka bryła - poza banalnymi przypadkami graniastosłupów i ostrosłupów znanych już licealistom - najczęściej ograniczona w podstawie pewną krzywą zamkniętą lub 4 krzywymi o znanych jawnych postaciach funkcyjnych lub krzywą i np. trzema ścianami o prostoliniowym przebiegu. Dopóki znana jest postać jawna funkcji, której wykresem jest powierzchnia z = f(x,y) będąca przekryciem budynku, to obliczenie objętości (kubatury) jest względnie proste. Wystarczy obliczyć całkę podwójną funkcji f(x,y) po obszarze D={ (x,y): ζ(t) ≤ x ≤ η(t), φ(t) ≤ y ≤ χ(t), t1 ≤ t ≤ t2}, gdzie t jest parametrem rzeczywistym, czyli

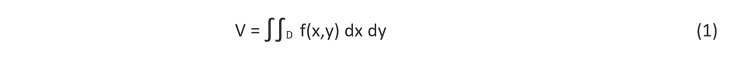
Problematyczne jest obliczenie kubatury budynku w przypadku, gdy trudno jest podać jawną postać funkcji f(x,y). Niemożność taka wynika np. z faktu, że przekrycie jest powierzchnią prostokreślną rozpiętą, w najprostszym przypadku pomiędzy odcinkiem AB o długości a (rys. 1 ) i krzywą przestrzenną określoną równaniami: x = t, y= μ(t), z = χ(t, μ(t)).

W tym przypadku kubatura jest określona wzorem

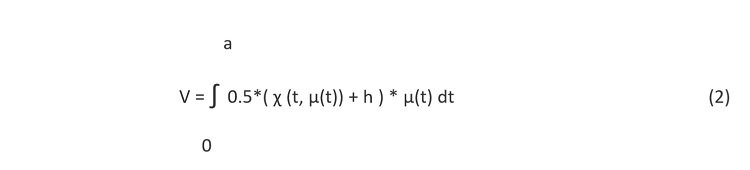
gdzie: h - wysokość odcinka AB leżącego na płaszczyźnie XOZ, χ(t, μ(t)) - krzywa przestrzenna będąca linią przenikania prostokreślnego przekrycia utworzonego z odcinków i prostokreślnej elewacji frontowej z krzywą μ(t) jako zarys rzutu prostokątnego tej elewacji na płaszczyznę XOY.

Rzeczywiste pole powierzchni dachu budynku z rys.1. będzie wyznaczone przy zastosowaniu uogólnionego twierdzenia Pappusa - Guldina, które orzeka, że pole powierzchni zakreślonej przez odcinek o zmiennej długości λ(t), przy przemieszczeniu go po trajektorii T o długości L (ortogonalnie do niej), jaką zakreśla środek masy odcinka, jest równe całce krzywoliniowej

gdzie: T - jest krzywą definiującą trajektorię dla wartości parametru 0 ≤ t ≤ a.

Pole powierzchni dachu na podstawie tego uogólnienia dane jest wzorem

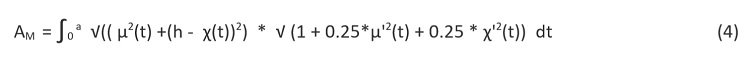
gdzie: μ'2(t) - ozn. kwadrat pochodnej funkcji μ(t) i χ'2(t) - kwadrat pochodnej funkcji χ(t).

Pole powierzchni elewacji frontowej jest równe całce krzywoliniowej

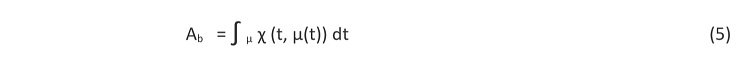
gdzie całkowanie odbywa się po krzywej μ(t). Zatem

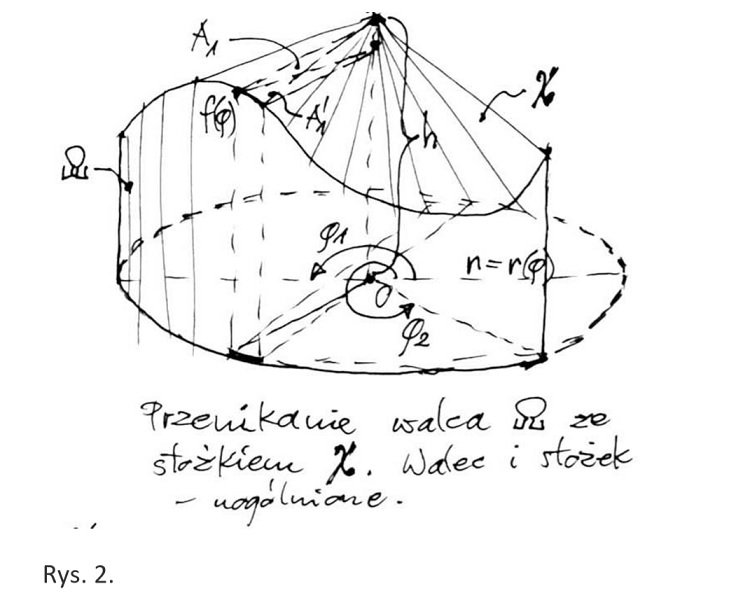
Jeśli mamy krzywą przestrzenną określoną równaniami: x = ζ(t), y= μ(t),

z = χ(ζ (t), μ(t)), dla t1 ≤ t ≤ t2, zaś dach jest uogólnionym stożkiem o wierzchołku W(0,0,h), elewację stanowi pobocznica uogólnionego walca, który w przecięciu z płaszczyzną XOY daje krzywą opisaną równaniami x = ζ(t), y= μ(t) - rys. 2.,

to kubatura takiej bryły jest określona wzorem

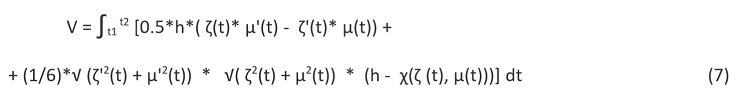
Rzeczywiste pole powierzchni dachu, czyli powierzchni prostokreślnej χ:

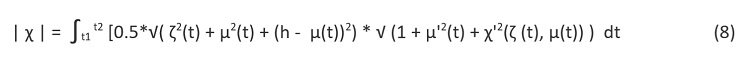
Rozważmy, jaką postać będą mieć wzory na objętość i pole powierzchni, jeśli krzywa zamknięta ograniczająca podstawę będzie miała postać r = r(ɸ) w biegunowym układzie współrzędnych, zaś krzywa przenikania dachu i elewacji z = f(ɸ, r(ɸ)) (rys. 2.).

Dla wyprowadzenia wzoru na objętość rozważamy elementarny fragment bryły i szacujemy jego objętość

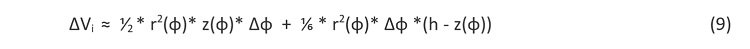
dalej tworzymy ciąg sum Riemanna

dla regularnej bryły granica takiego ciągu nie zależy od sposobu podziału bryły na elementarne części i po przejściu do granicy ciągu sum otrzymujemy całkę, która określa objętość bryły

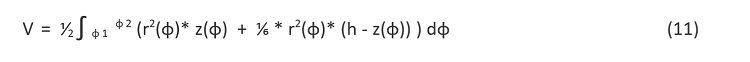
Pole powierzchni pobocznicy, zgodnie z geometryczną interpretacją całki krzywoliniowej

co po rozwinięciu daje

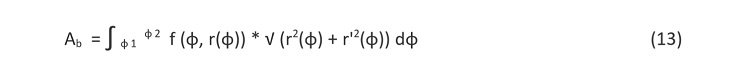
Pole powierzchni rzeczywistej dachu, będącego powierzchnią prostokreślną, wyznaczymy, rozważając stosowny ciąg sum Riemanna, przybliżający jego pole powierzchni elementarnymi trójkątami o podstawie ∆si (element łuku krzywej przestrzennej z = f (ɸ, r(ɸ))) i ramieniu równym odcinkowi łączącemu wierzchołek W(0,0,h) z punktem Pi na krzywej z = f (ɸ, r(ɸ)). Wobec tego, że

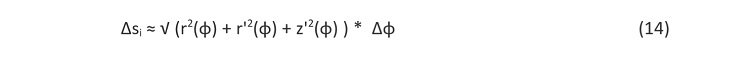
po przejściu do granicy mamy całkę reprezentującą pole powierzchni dachu w układzie współrzędnych biegunowych

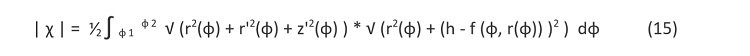
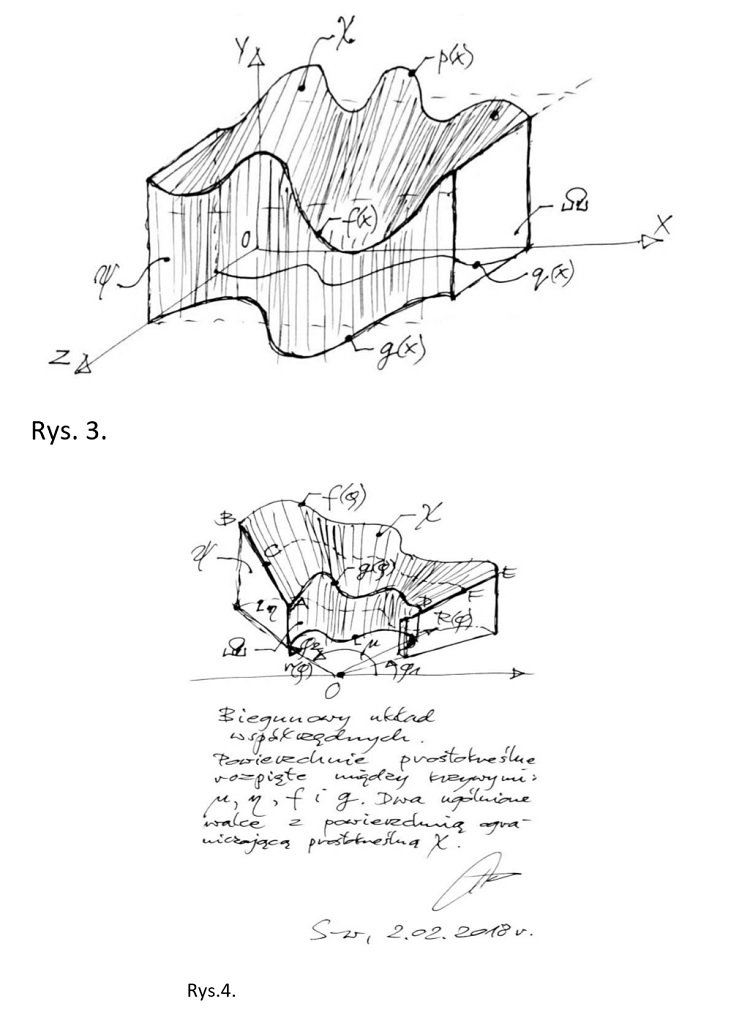
Kolejne ciekawe przykłady niekonwencjonalnych brył przedstawiam na rys. 3. i rys. 4.

Opracował:
mgr inż. Mirosław Matlęga
SOFT-POINT BIURO PROJEKTOWE