Superanaliza matematyczna

Niniejszą publikację dedykuję mojej kochanej żonie Marcelinie.

Wstęp

Do napisania niniejszej superanalizy matematycznej zainspirowała mnie lektura “Nadchodzi osobliwość” Raya Kurzweila. Autor rozważa w niej m.in. pięć paradygmatów wzrostu wykładniczego przetwarzania informacji i zauważa cyt.: “[...] w XXI wieku będziemy świadkami nie stu lat postępu technologicznego, ale postępu rzędu 20 tys. lat (oczywiście w stosunku do dzisiejszej szybkości postępu) lub tysiąc razy większego niż ten osiągnięty w XX wieku [...]”. Rozważania takie wymagają niejednokrotnie odpowiedzi na pytania typu: od którego momentu wzrost staje się gwałtowny? Wzrosty te są szybsze niż wzrost wykładniczy. Wprowadzone tutaj zostaje pojęcie kolana krzywej (miejsce, od którego wzrost staje się gwałtowny). Dla doprecyzowania pojęcia proponuję zdefiniowanie kolana krzywej jako punktu, w którym pierwsza pochodna osiąga wartość 1. Na potrzeby precyzyjnego i ścisłego opisu zjawisk zmieniających się w czasie wg funkcji np. y = exp(exp (ax+b)) konieczne stało się stworzenie aparatu pojęciowego, który prezentuję w dalszej części. Związane z zagadnieniami szybkiego wzrostu są również funkcje typu y= x^x i y= x^ (x^ x), dla których stworzyłem nową konwencję zapisu umożliwiającą np. podanie w jawnej postaci pierwiastka równania

czego dotychczas nie można było uczynić przy pomocy znanych konwencji zapisu, a jedynie podać jego przybliżenie uzyskane np. metodą bisekcji.

Wprowadzam nowe pojęcie: superpotęga - na oznaczenie działania analogicznego do pojęcia potęgi. Wyróżniamy tu podstawę superpotęgi i jej wykładnik. Pojęcie to umożliwia dogodny zapis funkcji charakteryzujących się wzrostem nieporównywalnie szybszym niż wykładniczy.

Przykładowo: funkcję y = x ^ (x ^ x) zapiszemy y = sp(x, 3) i odczytamy superpotęga o podstawie x i wykładniku 3. Stosuję konwencję zapisu: y równa się x do potęgi x do potęgi x. Natomiast pierwiastek równania (1) jako sp(3, 1/3). Wiele własności funkcji superpotęgowej jest podobnych do własności funkcji potęgowej. Wprowadzę również pojęcia: superpierwiastka, superlogarytmu, supersilni, supereksponenty, funkcji superwykładniczej oraz funkcji kaskadowej y = sp(x, x). Ta ostatnia ilustruje klasę funkcji o wzroście tak niebotycznie szybkim, że funkcje superpotęgowe rosną wolniej niż ona. Z drugiej strony funkcje superlogarytmiczne rosną tak wolno, że ich wzrost jest wolniejszy niż wzrost logarytmu naturalnego. Tego typu funkcje umożliwią konstrukcję “bajecznie szybkich” algorytmów do rozwiązywania zagadnień technicznych pozostających dotychczas poza zasięgiem możliwości. Być może posłużą one do opisu teorii fizycznych, które dopiero zostaną sformułowane, a będą wyjaśniać zjawiska obecnie niewyjaśnione.

Skoczów, 23.09.2017 r.

Spis treści

Pojęcie superpotęgi sp(x, n)

Superpotęga o wykładniku naturalnym.

Dziedziną D tej funkcji jest zbiór liczb rzeczywistych dodatnich R+ , przy czym dla n > 0 jej wartości y = sp (x, n).

Własności superpotęgi (dowody podane w załączniku)

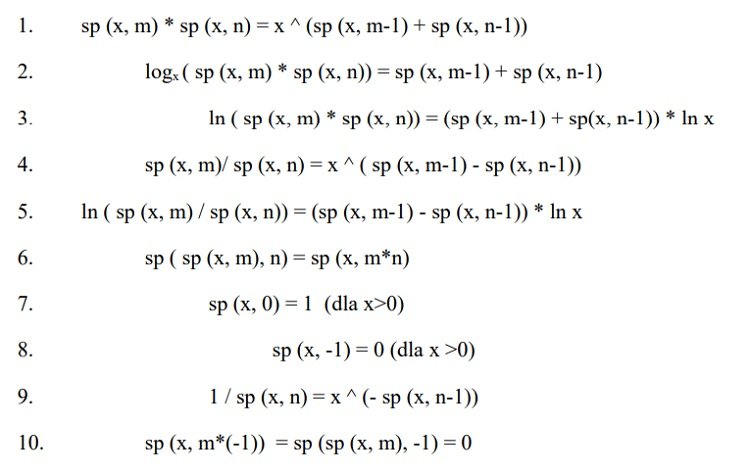
Twierdzenie 1.1. Pierwsza pochodna funkcji superpotęgowej jest dana wzorem rekurencyjnym dla dowolnego n naturalnego:

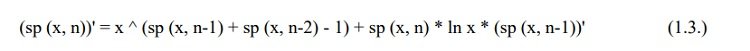
Dowód: (dowód podany w załączniku A).

Twierdzenie 1.2. Pierwsza pochodna funkcji superpotęgowej jest dana wzorem jawnym dla dowolnego n ≥ 3 (naturalnego):

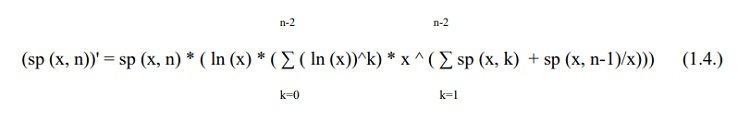
Dowód: (dowód podany w załączniku A).

Superpotęga o wykładniku całkowitym

Definicja 2. Superpotęgą x o wykładniku całkowitym p nazywamy liczbę

Mając zdefiniowaną superpotęgę o wykładniku całkowitym p, możemy zdefiniować funkcję superpotęgową o wykładniku całkowitym p jako

Dziedziną D tej funkcji jest zbiór liczb rzeczywistych dodatnich R+ , przy czym dla p < 0 przyjmuje wartość 0, dla p = 0 wartość 1 i dla p > 0 wartości y = sp (x, p).

Własności superpotęgi o wykładniku całkowitym to te same własności co dla n naturalnego (dowody podane w załączniku A).

Superpotęga o wykładniku ułamkowym (wymiernym)

Definicja 3. Superpotęgą x o wykładniku wymiernym p/q ≠ 0 nazywamy liczbę

Mając zdefiniowaną superpotęgę o wykładniku wymiernym p/q, możemy zdefiniować funkcję superpotęgową o wykładniku wymiernym p/q jako

Dziedziną D tej funkcji jest zbiór liczb rzeczywistych dodatnich R+, przy czym dla p/q < 0 przyjmuje wartość 0, dla p = 0 wartość 1 i dla p/q > 0 wartości y = sp (x, p/q).

Szczególny przypadek dla p = 1 i q > 0 nazywać będziemy superpierwiastkiem rzędu q, zapisując go

Mając zdefiniowaną superpotęgę o wykładniku wymiernym 1/q, możemy zdefiniować funkcję superpierwiastkową rzędu q jako

Własności wynikające wprost z definicji:

Superpotęga o wykładniku ułamkowym (wymiernym)

Definicja 4. Superpotęgą x o wykładniku rzeczywistym r nazywamy liczbę

Mając zdefiniowaną superpotęgę o wykładniku rzeczywistym r możemy zdefiniować funkcję superpotęgową o wykładniku rzeczywistym r jako

Dziedziną D tej funkcji jest zbiór liczb rzeczywistych dodatnich R+ , przy czym dla r < 0 przyjmuje wartość 0, dla r = 0 wartość 1 i dla r > 0 wartości y = sp (x, r).

Funkcją odwrotną funkcji superpotęgowej o wykładniku rzeczywistym r jest funkcja

Dziedziną D tej funkcji jest zbiór liczb rzeczywistych dodatnich R+.

Twierdzenie 1.3. Pierwsza pochodna funkcji y = sroot (x, 2) dana jest wzorem

Analiza trendów postępu technologicznego

Dla prowadzenia rozważań na temat trendów postępu technologicznego konieczne jest wprowadzenie pewnych funkcji charakteryzujących się wzrostem wolniejszym od logarytmu naturalnego oraz funkcji charakteryzujących się wzrostem niewiarygodnie szybkim - szybszym od wykładniczego. Poniżej definicje takich funkcji - przyznaję, że nie spotkałem w dostępnej literaturze ich definicji.

Superlogarytm o podstawie a ≠ 0.

Definicja 5. Superlogarytmem o podstawie a ≠ 0 liczby x nazywamy liczbę

Własności:

Supersilnia n(!) - definicja i własności

Definicja 2.1. Supersilnią n(!) nazywamy liczbę zdefiniowaną

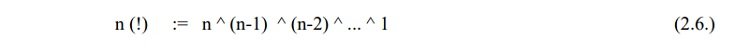
Przykładowym zastosowaniem pojęcia superpotęgi i superlogarytmu to możliwość podania precyzyjnego wyrażenia na n! w dodatku wygodniejszego niż wzór Stirlinga

Dowód. Mamy:

Własności:

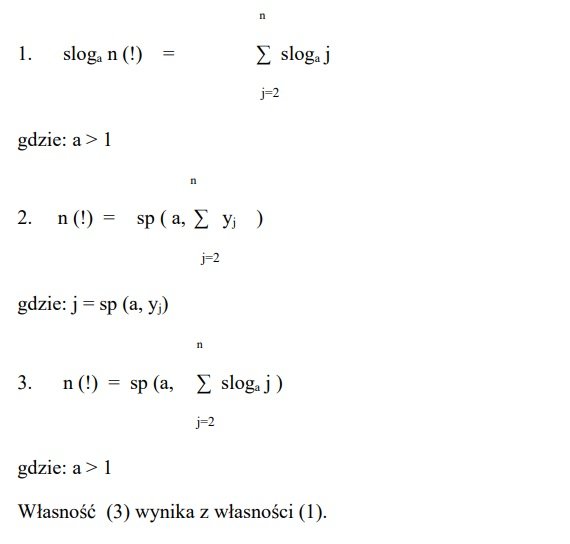
Supereksponenta y = sexp ( x, a, b)

Definicja 2.2. Supereksponentą nazywamy funkcję zdefiniowaną

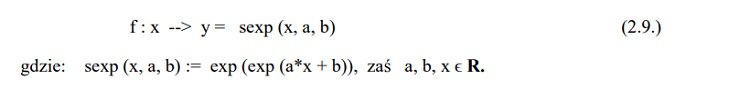
Wzrost wg supereksponenty jest charakterystyczny dla postępu technologicznego. W dalszej części pokażę na przykładzie wzrostu pojemności pamięci RAM, że następował on wg supereksponenty. Można go wykorzystać przy rozwiązywaniu zagadnień typu: w jakim roku pamięci RAM w komputerach osobistych osiągną 1 TB, jeśli wiadomo, że w roku 1993 RAM wynosił 4 MB, zaś w roku 2015 już 8 GB. Po wyznaczeniu krzywej regresji w postaci supereksponenty o parametrach: a = 0,085082 i b = -169,241784 dostajemy odpowiedź “w roku 2020”.

Mając wyznaczoną supereksponentę dla ww. zagadnienia, możemy także łatwo udzielić odpowiedzi na pytanie, od którego roku wzrost jest bardzo szybki. Wyznaczamy w tym celu tzw. kolano funkcji, czyli punkt, w którym f '(x) = 1.

Supereksponenta jako krzywa regresji

Lemat 2.1. Przez dowolne 2 różne punkty płaszczyzny R2 przechodzi dokładnie jedna supereksponenta y = sexp(x, a, b).

Dowód. Niech będą dane dwa różne punkty płaszczyzny P(x1, y1) i Q(x2, y2).

Logarytmujemy stronami zależność

Wyznaczenie kolana supereksponenty i jego znaczenie w analizie trendów

Złożenie funkcji liniowej i superpotęgi - wyznaczenie krzywej regresji.

Funkcja superwykładnicza y = sp (a, x) i badanie przebiegu jej zmienności.

Funkcja kaskadowa ψ(x) = sp (x, x) i jej pierwsza pochodna.

Załącznik A. Dowody własności

Opracował:
Mirosław Matlęga
SOFT-POINT BIURO PROJEKTOWE